In this wide-ranging conversation, Professor Behnam Pourhassan unpacks the intricate landscape of black hole thermodynamics and its profound implications for quantum gravity and cosmology. He explains how the entropy of a black hole is proportional to its surface area—a revelation that supports the holographic principle, which posits that information is encoded on boundaries rather than within volumes. The phenomenon of Hawking radiation, he notes, implies that black holes are not eternal but slowly evaporate over time.

Pourhassan delves into the thermodynamic phase transitions of black holes, explores quantum corrections to entropy, and examines the possibility of stable black hole remnants. He also discusses how dark energy propels the universe’s accelerated expansion and outlines how modified gravity theories seek to replace the notion of unseen substances with fundamental changes to gravity itself.

The conversation turns to the unique properties of anti-de Sitter (AdS) black holes and the role of the AdS/CFT correspondence, a theoretical bridge linking gravity to quantum field theory. Pourhassan also touches on a range of related topics—from cosmic strings and nonlinear electrodynamics to the statistical mechanics of gravitational systems and the implications of massive gravity for black hole physics. Crucially, he emphasizes the role of quantum information theory in addressing the black hole information paradox, a subject actively explored at the Canadian Quantum Research Center.

This interview will be featured in a volume of dialogues with leading thinkers in quantum cosmology, quantum gravity, and quantum information theory.

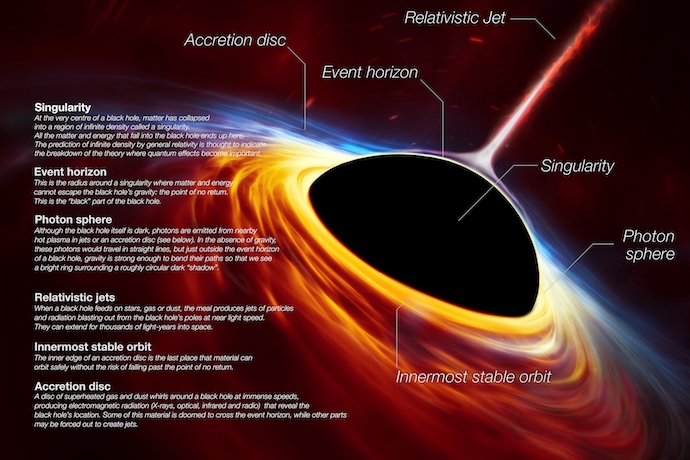
Scott Douglas Jacobsen: How is black hole entropy related to surface area? Why is this significant?

Behnam Pourhassan: Black hole entropy is directly proportional to its surface area, which is a remarkable and profound insight into the nature of quantum gravity. This relationship suggests that a black hole’s information content is encoded on its boundary rather than distributed throughout its volume. This is a key aspect of holography, a principle stating that the physics of a higher-dimensional space can be fully described by a theory existing on its lower-dimensional boundary.

This idea’s significance extends beyond black holes—it provides a deeper understanding of quantum gravity and spacetime itself. The fact that a black hole’s entropy is determined by its surface rather than its volume aligns with the holographic principle, which proposes that all the information contained within a region of space can be represented by data residing on its boundary.

This perspective has led to major advancements in theoretical physics, including the AdS/CFT correspondence, which links gravity in a higher-dimensional space to a lower-dimensional quantum field theory. The link between black hole entropy and surface area is not just about heat and energy. It suggests something deeper about how the universe works—possibly that space and time come from quantum information stored on surfaces.

Jacobsen: How is Hawking temperature calculated? What does this tell us about a black hole’s ultimate fate?

Pourhassan: Hawking temperature is found by studying how black holes emit radiation due to quantum effects near their event horizon. This radiation, known as Hawking radiation, causes the black hole to lose mass over time slowly. The temperature of this radiation depends on the black hole’s properties, such as its size and gravity. This has important consequences for a black hole’s fate. Since it continuously emits energy, it will gradually shrink and eventually evaporate completely if it doesn’t gain more mass from its surroundings. This suggests that black holes are not eternal and that their information content is crucial in understanding the deeper connections between gravity, quantum mechanics, and thermodynamics.

Jacobsen: How can black holes undergo phase transitions? Is this akin to regular materials? If so, what are the extreme conditions for these phase transitions?

Pourhassan: Black holes can undergo phase transitions similar to regular materials, such as water turning into ice or steam. In black hole physics, these transitions are often studied using thermodynamic properties like temperature, pressure, and entropy. For example, in anti-de Sitter (AdS) space, black holes can exhibit a phase transition similar to the liquid-gas transition, where a small black hole can grow into a large one as conditions change.

These phase transitions usually occur under extreme conditions, such as high curvature, strong quantum effects, or external forces like a surrounding thermal bath. Studying these transitions helps us understand deep connections between gravity, thermodynamics, and quantum mechanics.

Jacobsen: How do quantum effects modify the formulae of classical entropy? What are the implications of this derivation?

Pourhassan: Quantum effects introduce corrections to the classical entropy of a black hole, usually appearing as additional terms beyond the standard expression. These corrections arise due to quantum fluctuations near the event horizon, affecting how information and energy behave in extreme gravitational fields.

One key implication is that these modifications help address the information paradox by providing a deeper understanding of how entropy behaves at quantum scales. Additionally, these corrections suggest that black holes might not completely vanish upon evaporation but could leave behind a remnant or release information subtly.

Jacobsen: What are the logarithmic corrections to black hole entropy? Are there implications for stability?

Pourhassan: Logarithmic corrections to black hole entropy arise from quantum and thermal fluctuations near the event horizon. These corrections modify the classical entropy expression by adding a term proportional to the logarithm of the black hole’s area. They appear naturally in many approaches to quantum gravity, including string theory and loop quantum gravity. These corrections have important implications for black hole stability. They influence phase transitions, thermodynamic stability, and even the final stages of black hole evaporation. In some cases, they suggest that a black hole might reach a stable remnant instead of evaporating completely, which could have implications for the information paradox and quantum gravity.

Jacobsen: Does dark energy drive cosmic expansion? What is the lesser importance of this to physics and greater importance to cosmology?

Pourhassan: Yes, dark energy is currently understood to be the main driver of the universe’s accelerated expansion. It plays a central role in the Lambda Cold Dark Matter (ΛCDM) model, which is the standard model of cosmology. Cosmic expansion (i.e., the fact that the universe is expanding) results from the initial conditions set by the Big Bang. Dark energy, however, drives the universe’s accelerated expansion, which was discovered in the late 1990s through observations of distant Type Ia supernovae. In the equations of General Relativity, dark energy behaves like a cosmological constant (Λ) — a form of energy that exerts negative pressure, causing the expansion to speed up rather than slow down.

Dark energy doesn’t yet fit into the framework of particle physics. It doesn’t interact with matter or radiation (as far as we know), and it hasn’t been detected in lab experiments. It’s more of a placeholder concept: we see its effects but don’t know what it is. No current testable theories in quantum field theory or particle physics fully explain it.

Dark energy accounts for ~68% of the universe’s energy content. It dominates the cosmos’s fate and shape. So, even if we don’t know what dark energy is, cosmologists must include it to accurately model and understand the universe’s evolution.

Jacobsen: What are modified gravity theories?

Pourhassan: Modified gravity theories are alternative theories to Einstein’s General Relativity (GR) that attempt to explain gravitational phenomena — especially things like dark energy, dark matter, and cosmic acceleration — without invoking unknown substances or energy forms. Instead of saying, “There must be something weird like dark energy making the universe expand faster,” modified gravity theories say, “Maybe our understanding of gravity itself breaks down on large scales.”

Jacobsen: What distinguishes anti-de Sitter black holes from the generic idea of black holes?

Pourhassan: Great question. This touches on some deep ideas in theoretical physics, especially about where gravity meets quantum theory. When people say “black hole” generically, they usually mean one that exists in asymptotically flat spacetime — like in our observable universe, that includes Schwarzschild black holes (non-rotating, uncharged), Kerr black holes (rotating), and Reissner-Nordström black holes (charged), these solutions assume that far away from the black hole, space is flat (like our every day, large-scale view of the universe).

An AdS black hole exists in a universe with a negative cosmological constant — a curved background called Anti-de Sitter space. An AdS black hole is a solution to Einstein’s equations in this AdS background. So, AdS black holes differ from generic ones because they live in a negatively curved universe. That gives them very different boundary behavior and thermodynamic properties, making them especially important in theoretical frameworks like holography and quantum gravity.

Jacobsen: Is it possible to connect gravity with AdS/CFT correspondence in AdS space with quantum field theory?

Pourhassan: Yes — and that’s precisely what the AdS/CFT correspondence does: it connects gravity in AdS space with a quantum field theory (QFT) on its boundary. This is one of the most profound ideas in modern theoretical physics.

Proposed by Juan Maldacena in 1997, this conjecture says: A gravitational theory in (d+1)-dimensional AdS space is equivalent to a conformal field theory (CFT) living on its d-dimensional boundary. This is also called the holographic principle because A higher-dimensional gravitational theory (the bulk) is encoded by a lower-dimensional QFT (the boundary).

Jacobsen: How can mass in the graviton in massive gravity theories give insights into black holes and cosmic architecture?

Pourhassan: Massive gravity is a bold attempt to increase our understanding of gravity at a fundamental level, and giving the graviton a mass changes the rules of the game for how we think about black holes, cosmic structure, and even dark energy. In standard General Relativity, the graviton — the hypothetical quantum of gravity — is massless. Massive gravity theories propose that the graviton has a tiny but nonzero mass.

Black holes in massive gravity can differ from those in GR: They may not obey spherical solutions, which can be time-dependent. Unlike standard black holes, they can exhibit hair (i.e., non-trivial fields outside the event horizon). Their thermodynamics may change, affecting entropy and temperature. The gravitational field falls off differently — potentially modifying how black holes interact with surroundings or even merger dynamics (relevant for gravitational waves).

We might be able to test massive gravity through precision gravitational wave signals (like deviations in waveform tails or the speed of gravity). Adding mass to the graviton affects how gravity behaves on large (cosmic) scales: A massive graviton weakens gravity at large distances, mimicking the effects of dark energy. Some versions of massive gravity can explain the universe’s accelerating expansion without needing a cosmological constant.

Jacobsen: What is the holographic principle? What does this mean for an informational view of black holes?

Pourhassan: The holographic principle (named by Leonard Susskind) is a profound and somewhat mind-bending idea from theoretical physics. It suggests that all of the information contained within a volume of space can be represented as a hologram — a theory that lives on the boundary of that space. In other words, the 3D reality we perceive might be encoded on a distant 2D surface. This idea originated from efforts to understand black hole thermodynamics and quantum gravity, particularly the information paradox related to black holes. The holographic principle flips our intuition. It suggests that spacetime and gravity might emerge from more fundamental, lower-dimensional quantum information.

Black holes aren’t cosmic trash compactors that delete data — they’re more like storage devices that encode it in a holographic way.

Jacobsen: How do black hole thermodynamics compare to a van der Waals fluid?

Pourhassan: I like this question — this is where black holes get surprisingly thermodynamic and start acting like weird versions of everyday matter. Despite being exotic objects, black holes follow laws that look just like thermodynamics. Surprisingly, some black holes behave just like fluids — particularly a van der Waals gas. A van der Waals fluid is a more realistic model of a gas than the ideal gas law. It includes attraction between particles and a finite volume of molecules.

In AdS space, black holes can be put into thermal equilibrium with their surroundings. This setup gives them well-defined pressure, volume, temperature, and entropy like a fluid. Physicists like Robert B. Mann found that charged AdS black holes (like Reissner–Nordström-AdS) have thermodynamic behavior very similar to a van der Waals fluid. These black holes show first-order phase transitions between small and large black holes — just like the gas\liquid phase transition of ordinary matters.

Jacobsen: How does electric charge influence a black hole’s stability?

Pourhassan: Adding an electric charge to a black hole introduces new physical and thermodynamic behavior. A black hole with charge is called a Reissner–Nordström black hole (non-rotating) or Kerr–Newman (if rotating too). Its metric describes a black hole with mass , charge , and possibly spin . The presence of charge adds a repulsive term to the gravitational field. The resulting spacetime structure becomes more complex. In AdS spacetime, charged black holes show even more interesting behavior: They can be more thermodynamically stable than uncharged ones. There’s a stable equilibrium temperature, especially for larger charges and larger AdS radius.

Jacobsen: How does merging nonlinear electrodynamics with gravity modify black hole solutions? Do any new effects come from this merger?

Pourhassan: Merging nonlinear electrodynamics (NLED) with gravity leads to modifications in black hole solutions by altering the behavior of the electromagnetic field within the gravitational context. In traditional general relativity, black holes are described by solutions like the Schwarzschild or Reissner-Nordström metrics, where electromagnetic fields behave linearly (i.e., the field strength is directly proportional to the charge). However, when NLED is introduced, the relationship between the electromagnetic field and its source becomes nonlinear, affecting the structure of black holes.

This nonlinearity can lead to new phenomena, such as the presence of regular (non-singular) black holes, where the singularity at the center is avoided. Additionally, NLED can modify the black hole’s charge and mass distributions, potentially forming exotic black hole solutions with different thermodynamic properties, such as entropy or temperature behavior. In some cases, the introduction of nonlinear electromagnetic fields can lead to the existence of black holes with different horizons or altered stability properties, enhancing the range of possible black hole configurations and phenomena in gravitational physics.

Jacobsen: What are cosmic strings?

Pourhassan: Cosmic strings are hypothetical, one-dimensional defects in the fabric of space-time that may have formed in the early universe. These strings are incredibly thin but incredibly long, stretching across vast distances. They are remnants from the time just after the Big Bang, potentially created during phase transitions when the universe cooled and matter began to organize itself. Imagine them as incredibly dense, stretching lines of energy that may have significant gravitational effects on nearby objects. Although they haven’t been observed directly, cosmic strings interest scientists because they could provide insights into the fundamental forces of nature, like gravity, and help us understand the very origins of the universe.

Jacobsen: How can statistical mechanics illuminate the microscopic nature of gravitational systems?

Pourhassan: Statistical mechanics helps to understand the microscopic nature of gravitational systems by focusing on the collective behavior of a large number of particles, such as stars or gas molecules, that make up these systems. Instead of studying each particle individually, statistical mechanics examines how the overall system behaves by considering averages and probabilities. In gravitational systems, like galaxy clusters or black holes, the interactions between particles (such as stars or gas particles) are influenced by gravity, which is a long-range force. Statistical mechanics can reveal how these particles distribute, evolve, and form structures like galaxies or black holes. It connects the microscopic interactions at the particle level to macroscopic properties such as temperature, pressure, and density, helping us understand phenomena like the distribution of stars in a galaxy or the behavior of matter near black holes.

Jacobsen: How does quantum information theory inform gravitational physics studying black holes? How are these quantum research ventures pursued at the Canadian Quantum Research Center?

Pourhassan: Quantum information theory plays a crucial role in understanding the behavior of black holes, especially in the context of their thermodynamics and the famous information paradox. One key area of focus is how quantum information behaves in extreme gravitational fields, like those near black holes. Quantum mechanics suggests that information cannot be destroyed. Yet, classical interpretations of black holes—especially the idea of the “event horizon”—suggest that anything entering a black hole would be lost to the universe, which creates a paradox. Quantum information theory helps to explore potential resolutions, such as the idea that information might be encoded in the radiation emitted by black holes (Hawking radiation) or that black holes might have an intricate quantum structure that preserves information in ways not yet fully understood. This theory bridges quantum mechanics and general relativity, pushing scientists toward a unified theory of quantum gravity.

At the Canadian Quantum Research Center, researchers delve into quantum information science to understand these extreme quantum phenomena. They explore foundational concepts like quantum entanglement and superposition and how these might apply in the gravitational context of black holes. Researchers might also study quantum computing models or use quantum simulations to explore how information might behave at the event horizon or in a quantum gravity framework.

These efforts aim to shed light on some of the universe’s deepest mysteries by developing new theories and computational tools that could eventually help reconcile quantum mechanics with the general theory of relativity.

Jacobsen: Thank you for the opportunity and your time, Behnam.

Pourhassan: Thank you for the professional questions. I should add that the answers to most of these questions related to black hole thermodynamics are explored in detail in my book, Thermodynamics of Quantum Black Holes: Holography, which will be available online soon.